El problema de Waring

En ocasiones puede resultar paradójico que la respuesta a una pregunta suponga la aparición de muchas otras preguntas, pero en matemáticas esto ocurre constantemente. Es habitual que la demostración de un hecho traiga consigo la formulación de muchas preguntas relacionadas con este hecho.

Edward Waring

Precisamente esto es lo que ocurrió en 1909. Ese año David Hilbert daba una demostración de una conjetura conocida como problema de Waring, formulada por el matemático inglés Edward Waring más de cien años antes, en 1770.

En concreto, Waring conjeturó en su obra Meditationes Algebraicae que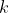

Todo entero positivo puede expresarse como suma de a lo sumo potencias -ésimas positivas, siendo dependiente de (se entiende que es un número entero positivo).

Esto quiere decir que dado un exponente entero positivo , todo número entero positivo que tomemos necesitará de, como mucho, un número concreto de potencias con ese exponente 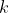. Waring conjeturó que todo entero positivo puede expresarse como suma de, a lo sumo, 4 cuadrados, 9 cubos y 19 potencias cuartas. Vamos, que si expresáramos todos los enteros positivo como suma de números al cuadrado, no haría falta usar 5 de ellos para expresar así ningún número.
Al parecer no se considera que Waring tuviera la suficiente capacidad para probar su propia conjetura, de hecho ni siquiera para probar alguno de los casos particulares () que él mismo conjeturó. Pero ahí quedó la cosa, como un reto al igual que cualquier otra conjetura, para quien la quisiera tomar.
El mismo año 1770 en el que se formuló la conjetura, el caso queda demostrado por Lagrange dando como resultado que Waring tenía razón: todo entero positivo puede expresarse como suma de, a lo sumo, 4 cuadrados. Como no podía ser de otra forma, este resultado se denomina teorema de los cuatro cuadrados y, aunque Fermat ya pensaba que era cierto, fue Lagrange el primero en dar una demostración. Un punto para Waring. Pequeño, sí, pero ahí queda.

David Hilbert

La traca final llegó en 1909 cuando Hilbert demuestra el caso general. Es decir, dado cualquier entero positivo 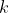, el número 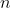de potencias 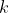-ésimas que hay que sumar para obtener cualquier entero positivo está acotado, tiene un máximo, un tope, sea cual sea el número entero positivo que queramos expresar así.

El pero de todo esto (sí, siempre tiene que haber un pero) es que la demostración de Hilbert no da ningún procedimiento para calcular ese número máximo de sumandos. Por poner un ejemplo, esto quiere decir que sabemos que todo número natural puede ser expresado como, a lo sumo, un cierto número concreto de potencias de exponente , pero la demostración de ello no nos dice cuál es ese número concreto de ellas.
Dado que no tenemos una fórmula explícita para, dado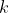 , calcular el valor de 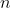, la única opción que nos queda es estudiar caso por caso: cuadrados por un lado, cubos por otro, potencias cuartas, etc.

Dado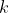 , este valor 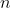se denota como . La definición podría ser así:

Dado , denotamos por al mínimo número de -ésimas potencias que hacen falta para representar todos los números naturales como suma de ellas.

Es evidente entonces que . Y, por el teorema de los cuatros cuadrados, sabemos que (es decir, hacen falta como mucho 4 cuadrados para representar todos los números naturales como suma de ellos).
¿Qué otros valores de se conocen? Pues estos:

• , demostrado por Wieferich yKempner entre 1909 y 1912.
• , demostrado por Balasubramanian, Dress y Deshouillers en 1986.
• , demostrado por Chen Jingrun en 1964.
• , demostrado por Pillai en 1940.

Primero: dos puntos más para Waring. Igual es cierto que no tenía suficiente capacidad matemática para demostrar su conjetura, pero el tío dio en el clavo con ella, acertó los tres valores. Algo es.
Segundo: curioso el hecho de que se encontrara antes que , y éste a su vez antes que .
¿Qué ocurre con el resto de valores? Bueno, poco a poco se fue obteniendo información sobre ellos. J. A. Euler, hijo mayor de Leonahrd Euler (según MathWorld), demostró que una cota inferior para era la siguiente:

Si utilizamos esta fórmula para calcular las cotas inferiores para los casos que ya conocemos obtenemos…que para la cota es 4, para es 9, para es 19, para es 37 y para es 73. Un momento, ¿esos no son exactamente los valores de ? Pues sí.
De hecho se conjetura que el valor exacto de es exactamente el que da esa cota. Mahler demostró en 1957 que como mucho hay un número finito de valores de 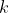para los cuales es mayor que esa cota. De todas formas de ahí a que tenga exactamente ese valor va un trecho.
Pero este problema todavía da para más. Hay otro número asociado al problema de Waring que tiene interés. Se denota , y representa lo siguiente:

Dado , llamamos al número mínimo de potencias -ésimas necesarias para expresar todos los enteros positivos, desde un cierto entero en adelante.

Para entender mejor qué es esta (y sobre todo para no confundirla con ) vamos a estudiar el caso . Hemos visto antes que , pero en realidad hay muy pocos números enteros que necesitan una suma de 9 cubos para expresarlos. De hecho sólo hay dos, 23 y 239. Por ello ahora tendríamos que (ya que a partir de 239 todos los números enteros pueden expresarse con, como mucho, 8 cubos). Pero más adelante se demostró que hay solamente 15 números enteros que necesitan 8 cubos:

y

Este hecho rebaja el valor de a, como mucho, 7. Por tanto ahora tenemos que . Y aquí nos quedamos, ya que en este caso no se han realizado más avances.
Para el caso sí se tienen más datos. De hecho se conoce que . De ahí en adelante sólo se conocen cotas para este . En el enlace de MathWorld que hay al final podéis ver una tabla con valores de y cotas para .
Para terminar, comentar que existen otras variantes de este problema que abren nuevos campos de investigación. La más obvia consiste en considerar también la posibilidad de que aparezcan potencias de números enteros negativos. En esta variante, la demostración de la existencia del primer valor comentado anteriormente, denominado ahora , es más fácil que en el problema clásico, pero es mucho más complicado determinar su valor en cada caso. De hecho sólo se conoce para , siendo . En este problema también tenemos un segundo valor, llamado , que también se conoce solamente para , siendo también .